How to Measure the Size of Earth with a Stick

Each Spring and Autumn Equinox, we're able to measure the diameter of the Earth. How?

All you need is:

• a stick (a toilet plunger works!)
• a measuring tape
• a flat outdoor surface
• a clear sky at solar noon

In Spring 2021, I did a live stream of this experiment in real-time. I've embedded the video below:

How this works

This is called the 'Eratosthenes Experiment'. In short, if you were to be at the Equator on the Equinox at solar noon, the Sun would be directly overhead. No shadow would be cast from object around you.

But if you were not at the Equator – say 1000 kilometres north of the Equator – at solar noon, you would see shadows cast.

If you were to measure the size of those shadows and also knew how far from the Equator you were, you would have all the info you need to measure the Earth.

Sounds crazy? It kinda is. And I love it.

Carl Sagan explains this story more poetically:

How to Do It

1) Find what day

This experiment is best done exactly on the Spring or Autumn Equinox. This day changes year-by-year, but is generally around March 20 or September 22. This page should help you out.

2) Find what time / solar noon

This experiment needs to be done when the Sun is exactly South from your location. This is called "solar noon".

This differs from 12:00 PM noon on your clock.

To find it, go to this link and search for your city/town. Then, scroll down to the date for the Equinox, and in the far right of the table, you'll see a column called "Solar Noon".

For example, on September 22, 2022 in Montréal, solar noon is 12:46 PM ET. This is the time that I would take my measurements.

3) Ready and measure your stick

We are going to use a stick during this experiment. It is important this stick is straight and can stand upright.

In my case, yes, I used a plunger. Looks silly, but works perfectly.

Measure the length of your stick, as we are going to use this number. In my case, my plunger was 59 cm long.

4) Find a flat surface outdoors

This is also important. Find a flat, outdoor surface, like a parking lot. Make sure at solar noon, you'll have a clear view of the Sun. Make sure you do this in advance, as we don't want to be scrambling when the moment comes.

I was lucky and was able to do this on the sidewalk in front of my apartment.

5) Measure stick shadow at solar noon

OK, the time has come. A few minutes before solar noon, head outside and have your stick upright. Make sure isn't leaning one way or the other.

At exactly solar noon, measure the length of the shadow that it creates.

Note: if you're using a plunger, make sure your measure from the "centre" of the plunger.

Write your measurement down! In Montréal on the Equinox, my measurement was 57 cm, but yours will differ depending on your latitude and stick length.

6) Draw out your measurements on a triangle

Let's pause for a moment and consider what data we have: the length of our stick (59 cm), and the length of the shadow of our stick (57 cm).

But we also have another piece of data: an angle of a triangle (90°).

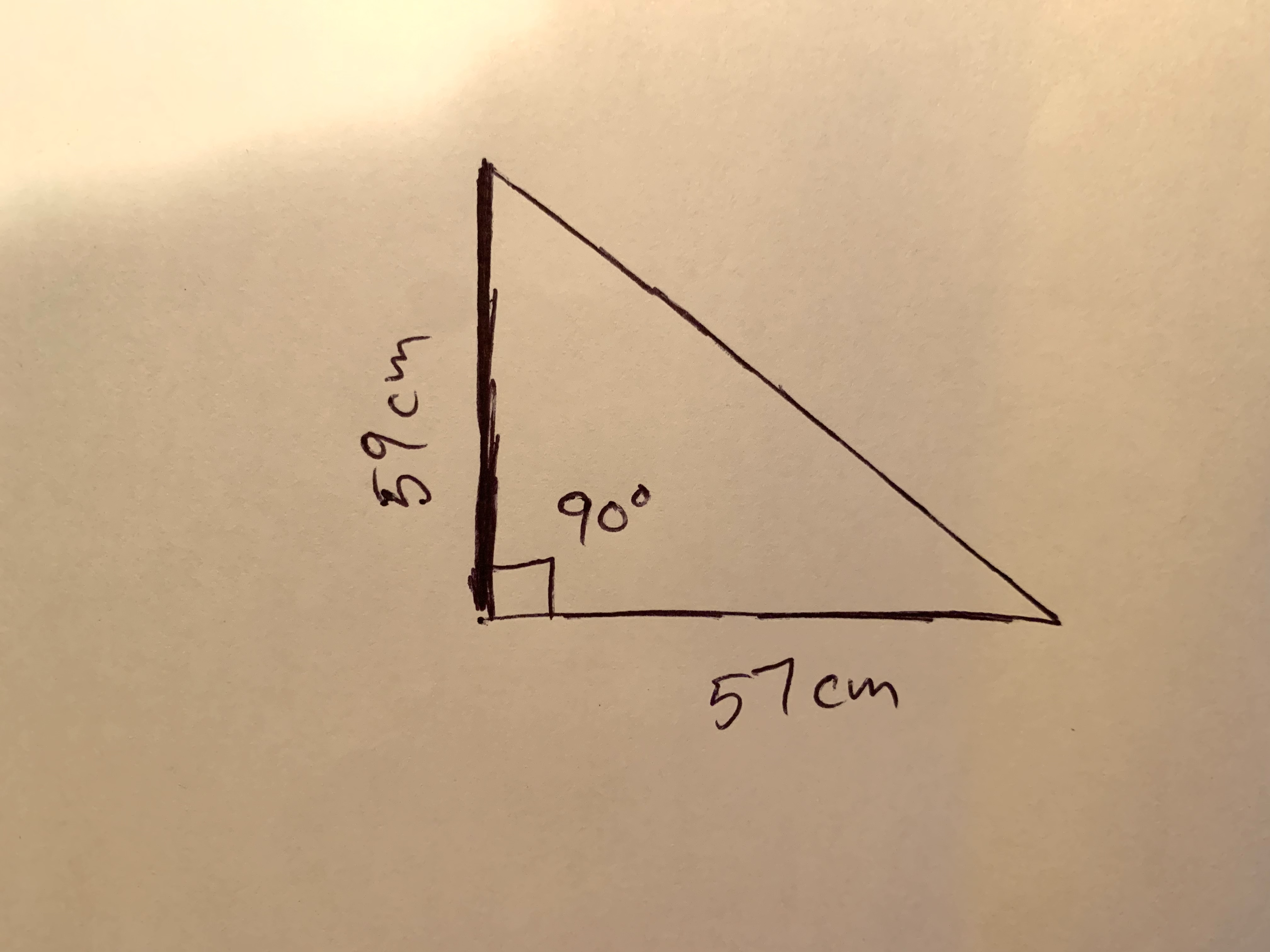
Why is this important? I beg for your imagination for a moment...

Imagine that our stick extended all the way to the centre of the Earth. Then, imagine another stick at the Equator doing the same thing.

When the intersect at the centre of the Earth, they'll make another angle. I've outlined it in yellow in the diagram below:

This yellow angle is really cool. And frankly, blew me away when I did this experiment for the first time in 2020.

This yellow angle tells us how far from the Equator we are in degrees. It tell us our latitude! So how can we find this value out?

We have all the data we need with our triangle info from above.

7) Find rest of triangle info

If you're a high school teacher and want your students to do this the old fashioned way, that's cool. But for me, I'm going to use a Triangle Calculator.

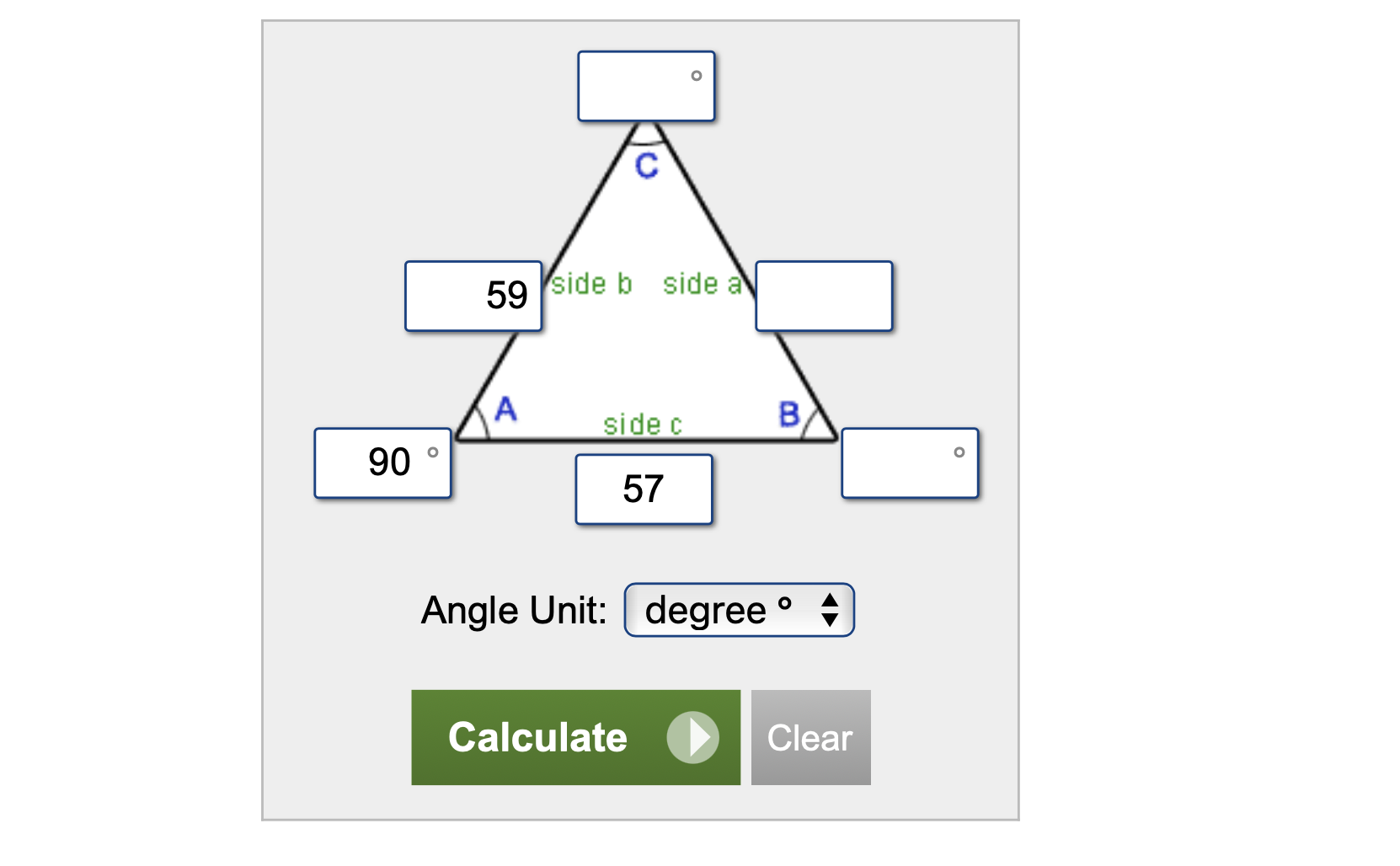
I'm going to use this tool and plug in this data:

• length of stick (59)
• length of stick shadow (57)
• angle from ground and stick (90°)

Here was it looked like when I put the data in:

And here was the result that I got back:

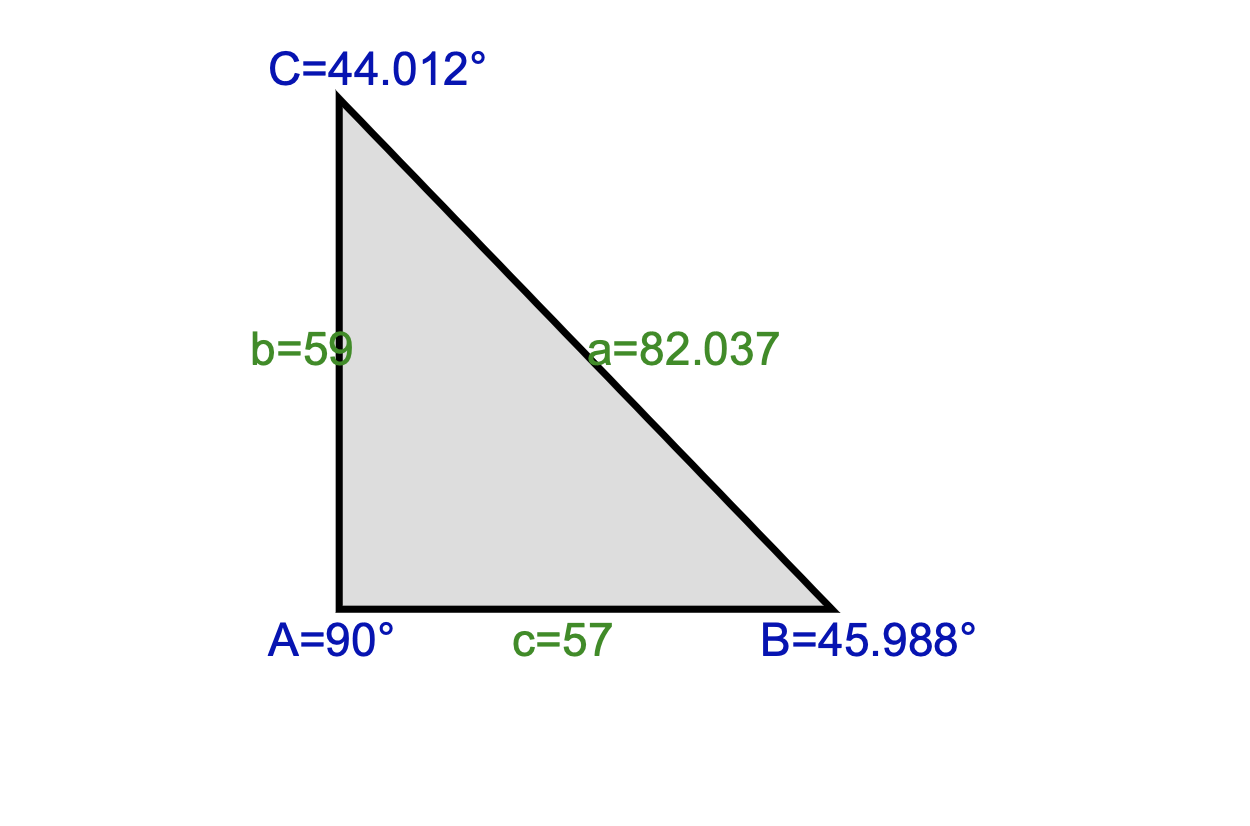
8) Find Angle C / Latitude

See that Angle C, 44.012°? That's our special angle!

This is where I must admit, I'm not a math teacher. However, one of my YouTube viewers put it succinctly: "​The rule is, if you have two adjacent triangles, if they have one of their sides parallel to each other, their opposite angles are identical. It's a triangle property."

Good enough for me!

But importantly, that angle is equal to the angle that our sticks at the centre of the Earth makes. This, incredibly, tells us our latitude on Earth (roughly, of course).

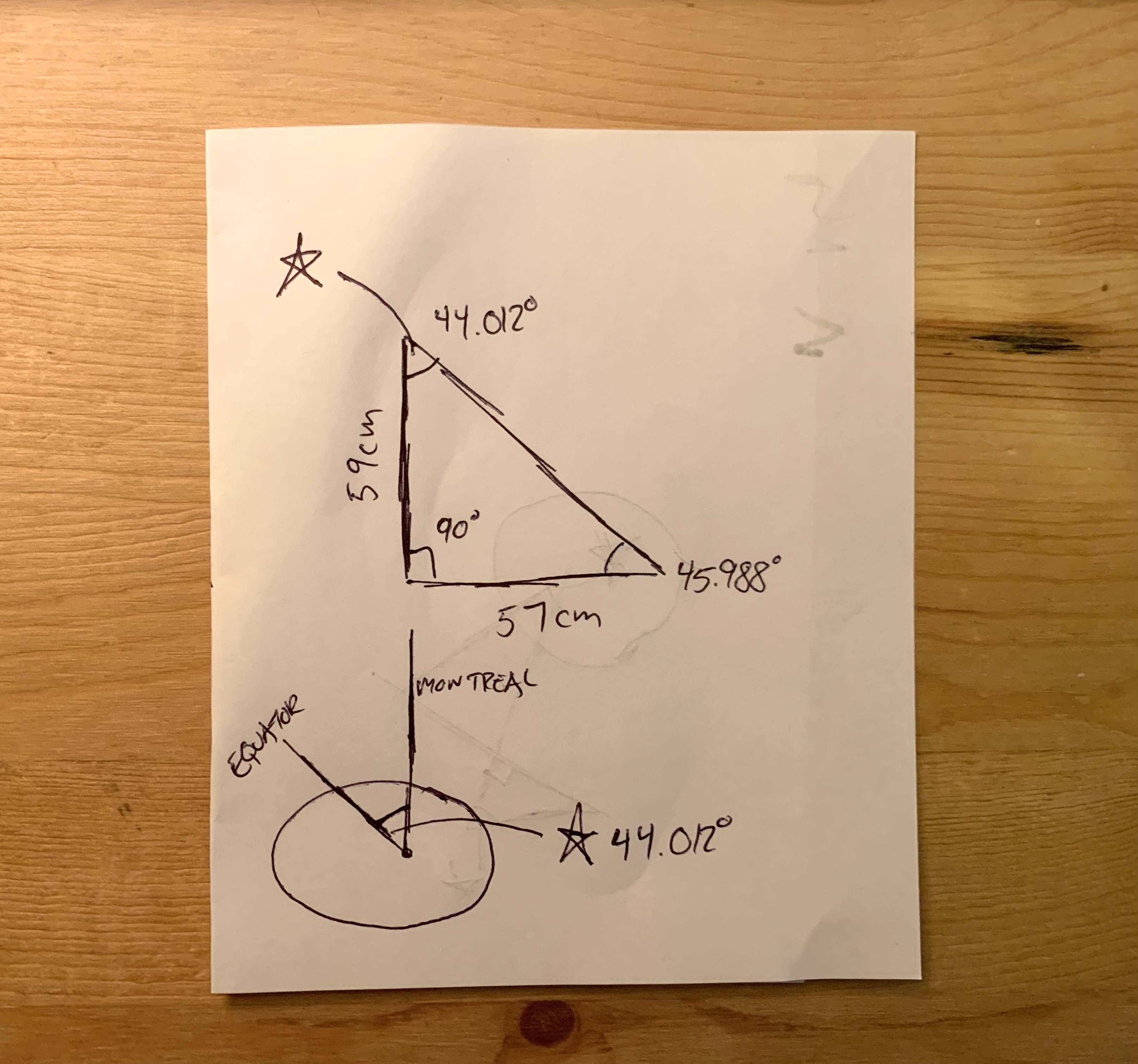
My latitude in Montréal is 45.5019°. Admittedly, this measurement is off by over 1°.

Keep in mind, though, we're measuring this with a toiler plunger. So the plunger could have been slightly tilted, the shadow might have actually been 58 cm, etc... Still, this is close enough for me.

The important thing is that we find this angle.

9) Find distance to Equator

We need one last value: our distance to the Equator.

The legend of Eratosthenes says the he hired somebody to pace out and measure the distance from Alexandria to Syene, where another measurement was taken. That's... kinda nuts.

We are not going to walk to the Equator. Instead, we're gonna Google Maps to find our distance.

To do this, right-click on your location, then click 'Measure distance':

Then, zoom far out so you can see the Equator. Click on the Equator so that it makes a straight line, like so: 

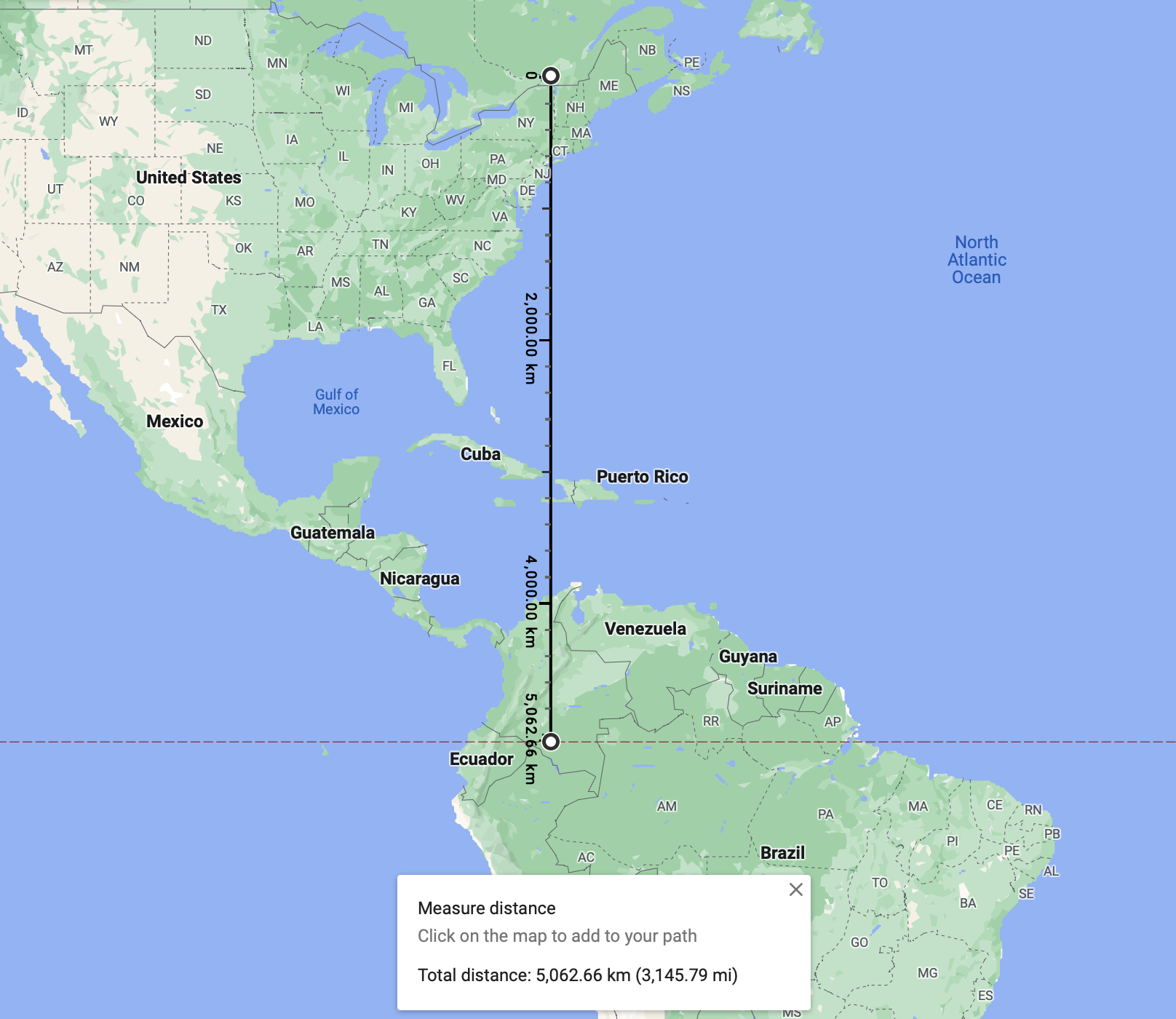
At the bottom, it will say "Total distance". In my case, this is 5,062 kilometres.

10) Plug into Equation

The last step! We have all the info we need.

We are going to use this equation to find the distance of Earth:

360 * distance / angle

Let's plug our values in

(360 * 5062) / 44.012 = 41,405 kms

There it is!

Our final value was 41,405 kilometres!

Compare with Reality

The actual circumference of the Earth is 40,075 kilometres. Our value is about 3% off from this.

That, to me, is still remarkable. Using a toilet plunger, we've gotten remarkably close to finding out how big the Earth actually is.

As mentioned above, I could have used a more accurate measuring device. I also could have made a small error in measuring the shadow and got a more accurate result.

But this is what you can expect when you do this experiment: get very close to finding the size of Earth using simple tools.